Üye Girişi
Bağlan Google+ ile Bağlan Facebook ile Bağlan
Yeni Kayıt
Tüm Forumlar
  • Tüm Forumlar
  • Web Tasarım - Programlama
  • Yazılım Geliştirme
  • Yazılım Geliştirme Sohbet Bölümü
  • Bu Konuda
Şimdi Ara

Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları (10. sayfa)

Sıcak Fırsatlarda Tıklananlar
Editörün Seçtiği Fırsatlar
Daha Fazla
Bu Konudaki Kullanıcılar: Daha Az
2 Misafir - 2 Masaüstü
5 sn
211
Cevap
19
Favori
12.356
Tıklama
Daha Fazla
İstatistik
  • Konu İstatistikleri Yükleniyor
Konuya Özel
7 oy
Öne Çıkar
Cevapla
Sayfa: önceki 7891011
Sayfaya Git
Git
sonraki
Giriş
Mesaj
  • Tuğkan-0153 kullanıcısına yanıt

    bozuk paraların ödemeyi eksiksiz karşılaması koşuluyla çözüm:


    Kod 
    Yığını:
    def bozuk_para(toplam, para_tipleri):
    # para_tipleri 'nin tam toplam yapması koşulu ile !
    paralar=[]
    while toplam > 0:
        para = max([c for c in para_tipleri if c <= toplam])
        paralar.append(para)
        toplam -= para
    return paralar

toplam=14
para_tipleri=[1,3,5]
para_tipleri_str=','.join(map(str, para_tipleri))
sonuc=bozuk_para(toplam, para_tipleri)
sonuc_str='+'.join(map(str, sonuc))
print(toplam, "'i ", para_tipleri_str, " ile odemek icin:", sonuc_str)

    b şıkkı için de len(sonuc) yeterli :)


    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:41:12 >

  • Burada a şıkkının çözümü olduğunu düşünmüyorum a şıkkı şu şekilde çözülebilir :



    Kod 
    Yığını:
    def solve(toplam, para_tipleri):
    dp = [[] for i in range(toplam + 1)]
    dp[0] = [[]]
    
    for i in range(len(para_tipleri)) :
        for j in range(para_tipleri[i] , toplam + 1) :
            dp[j] += [ z +[para_tipleri[i]] for z in dp[j - para_tipleri[i]] ]  
    
    return dp[toplam]

print( solve(13, [1, 3, 5]) ) 
            
    < Bu ileti mobil sürüm kullanılarak atıldı >
  • Ec jok E kullanıcısına yanıt
    Kodu incelemeden direkt denedim.

    [[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3], [1, 1, 1, 1, 1, 1, 1, 3, 3], [1, 1, 1, 1, 3, 3, 3], [1, 3, 3, 3, 3], [1, 1, 1, 1, 1, 1, 1, 1, 5], [1, 1, 1, 1, 1, 3, 5], [1, 1, 3, 3, 5], [1, 1, 1, 5, 5], [3, 5, 5]]
    2

    biçiminde çıktı verdi.

    İlk çıktı uzun de anlaşılmaz bir liste.

    İkinci çıktı "2" toplam bozuk para sayısını veriyor ise, yanlış. 13 = 5 + 5 + 3 ile 3 olmalı.



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:43:16 >
    < Bu ileti mini sürüm kullanılarak atıldı >
  • 2 yi vermemesi lazım sizin kodlardan kalan bir şey olabilir mi o
    İlki ise bu toplamı elde edebileceğimiz tüm kombinasyonlar listesini veriyor

    < Bu ileti Android uygulamasından atıldı >
  • Ec jok E kullanıcısına yanıt
    Ta kendisi, benim kodların sonucu o. Başka bir işe bakarken hızlıca denediğim için görmedim :)
    Kod güzel. Peki bu çözümü recursion stilinde de yapabilir misiniz ?



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:44:30 >
    < Bu ileti mini sürüm kullanılarak atıldı >

  • Ona bakacağım kaptan, ama en önemli sorunu hallettem gerekiyor,

    Anlaşılan, Sende bir haller var! uzun zamandır girmiyorsun! inşaallah başına ciddi bir şey gelmemiştir.


    < Bu mesaj bu kişi tarafından değiştirildi berce -- 15 Ağustos 2021; 2:23:34 > 
  • Kod 
    Yığını:
    bool isPrime( int number ){

    if( number == 2 )
        return true;
    else if( number == 0 || number == 1 || number % 2 == 0 )
        return false;    
    else if( number >= 3 ){

        for( int i = 3; i * i <= number; i += 2 ){

            if( number % i == 0 )
                return false;
        }
        return true;
    }    
}


bool findTwoPrime( int numbers[], int arrSize ){

    for( int k = 0; k < arrSize; ++k ){

        for( int i = 2; i <= numbers[k] / 2; ++i){

            if( isPrime(i) && isPrime( numbers[k] - i ) ){
    
                printf("%d -> %d + %d \n", numbers[k], i, numbers[k] - i);
                break;
            }
        }
    }
    
}


    int numbers[] = {28, 36, 52, 112, 442 };

    findTwoPrime(numbers, 5);


    Hocam üstte arkadaşın yazdığı programa biraz eklemeler yaptım.




  • BL3E kullanıcısına yanıt
    Esasında bu soru oldukça kolay cunku çözüm için yalın bir teori olan Goldbach konjektürünü döngü ile kodlamak yeterli.

    Şu soruyu (bozuk para problemi / coin change problem) recursion kullanarak çözebilir misiniz ?

    https://forum.donanimhaber.com/reddit-hn-euler-vs-sitelerdeki-mulakat-odev-ve-algoritma-sorulari--139462992-9#149690350

    Bu soruyu bir kişi döngü ile çözdü (yukarda) ancak çözümü Internette biryerden almış, dolayısıyla gerçek çözüm sayılmaz.

    Bu sorunun döngüyle çözümü Internette bayagı bir var ancak recursion ile çözümü pek yok :)



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 30 Eylül 2021; 1:21:12 >
    < Bu ileti mini sürüm kullanılarak atıldı >




  • Coin Change | DP-7 - GeeksforGeeks

    Coin Change Problem Number of ways to get total | Dynamic Programming | Algorithms - YouTube


    Üstteki linklerde çözümleri var fakat ben birşey anlamadım. Tablo ile çözmüşde neden bu tabloyu oluşturdu ? Ekstaradan tablonun da kendi içinde kuralı var. Onun haricinde çözümü internetten kopyalayıp buraya yapıştırmak marifet değil ki yoksa tonla çözüm var internette.


    < Bu mesaj bu kişi tarafından değiştirildi BL3E -- 1 Ekim 2021; 20:8:6 >




  • BL3E kullanıcısına yanıt
    İlk çözüm recursion kullanmakla birlikte sonuç olarak yalnızca bozuk para kombinasyonlarının toplamını döndürüyor. Soruya, bozuk para kombinasyonlarının kendisinin de gösterilmesini ekledim dolayısıyla bu çözüm eksik oldu :) Buradaki amacım, Internetteki çözümlerden cok kişinin kendi çözümünü geliştirmesi :)

    İkinci çözüm dynamic programming / DP denilen yöntemi kullanıyor, oradaki tablo DP'yi açıklamak için. Coin Change probleminde kombinasyon cok sayıda olmadıgı sürece DP kullanılmak zorunda değil. Kombinasyon cok sayıda olsa bile yine zorunda değil ancak bilgisayarın kısa sürede buldurması için DP. Burada Coin Change problemi kapsamında alt konu olarak anlatıldığından anlamak zor olabilir. DP'ye özel videolardan DP konusunu daha iyi anlayabilirsin



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:46:11 >
    < Bu ileti mini sürüm kullanılarak atıldı >

  • CCC + BBB + AAA = CAAB ise, A, B, C imlerini recursion (özyineleme) kullanarak bulunuz. İmlerin hepsi birbirinden değişik olup 1-9 arası sayılardır.


    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 30 Ocak 2022; 21:12:14 >

  • goldbach sanısı çözüldü isteyen arkadaş aşağıdaki linkten çözüm dosyasını okuyabilir


    https://onedrive.live.com/view.aspx?resid=F5A3AB27C45DB054!1083&ithint=file%2cdocx&authkey=!AF_vNMXzBkvX_X8


    yukardaki sayıların cevap resimlerini excel ile yaptığım proğramdan atıyorum

    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları


    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları


    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları


    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları


    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları








  • GOLDBACH SANISI ÇÖZÜLDÜ

    https://onedrive.live.com/redir?resid=F5A3AB27C45DB054!1083&authkey=!AF_vNMXzBkvX_X8&ithint=file%2cdocx
  • doktor0906 D kullanıcısına yanıt
    Baktım yalnız o Goldbach Konjonktüründen başka bir nes gibi göründü
    https://en.wikipedia.org/wiki/Goldbach's_conjecture

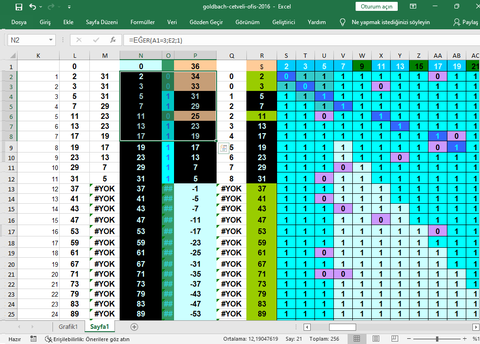
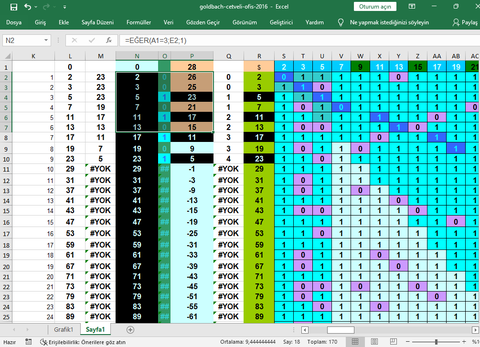
    2'den büyük her düz sayı, iki asal sayının toplamı olarak yazılabilir savının doğru olup olmadığını 28, 36, 52, 112, 442 sayı listesi için göstermek. Bizim problem bu. Senin çözümde bu yönde bir içerik göremedim. Bu arada sorunun çözümünü, soruyu gönderdikten birkaç ay sonra şuradahttps://forum.donanimhaber.com/reddit-hn-euler-dh-gibi-sitelerden-is-gorusmesi-sorulari-odev-sorulari--139462992-9#145215773 SS olarak göndermişim, SS'e kısa notlar ekli yeni versiyonu: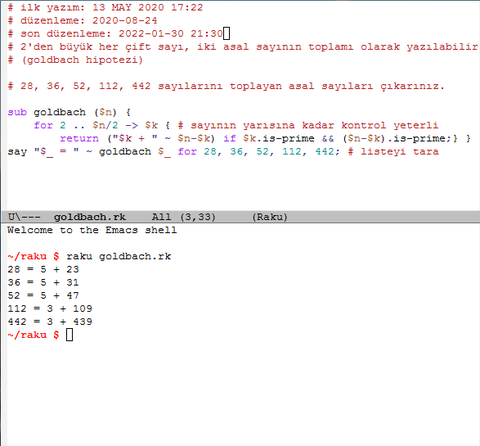

    Reddit, HN, Euler, DH gibi sitelerden iş görüşmesi soruları + ödev soruları



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:47:28 >
    < Bu ileti mini sürüm kullanılarak atıldı >




  • doktor0906 D kullanıcısına yanıt
    Yanıtladığın

    CCC + BBB + AAA = CAAB ise, A, B, C imlerini recursion (özyineleme) kullanarak bulunuz. İmlerin hepsi birbirinden değişik olup 1-9 arası sayılardır.

    sorusuna şu ana dek (Farsça: henüz) yanıt gönderen yok. Bu soruya çözüm gönderebilir misin ? Çözüm (kod) özyineleme / recursion ile yapılmalı.



    < Bu mesaj bu kişi tarafından değiştirildi Tuğkan-0153 -- 11 Ağustos 2022; 12:50:9 >
    < Bu ileti mini sürüm kullanılarak atıldı >

  • C=1

    B=8

    A=9

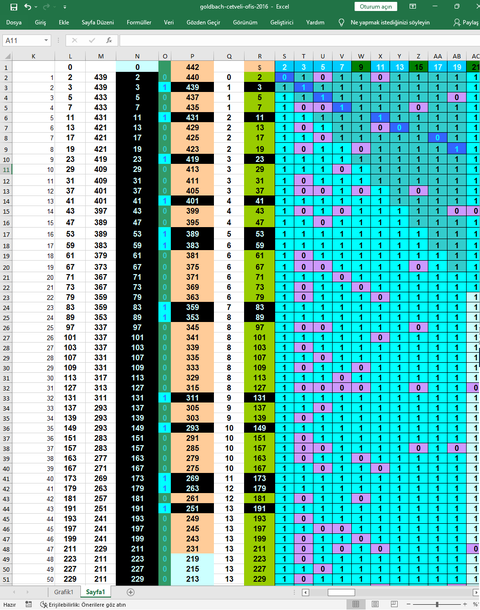
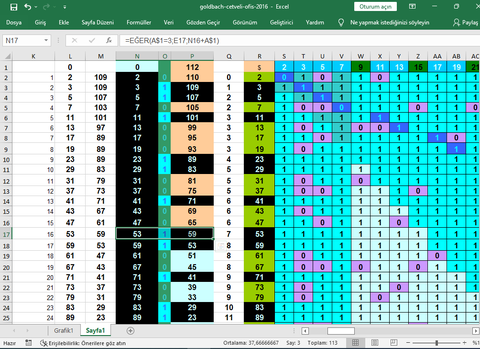
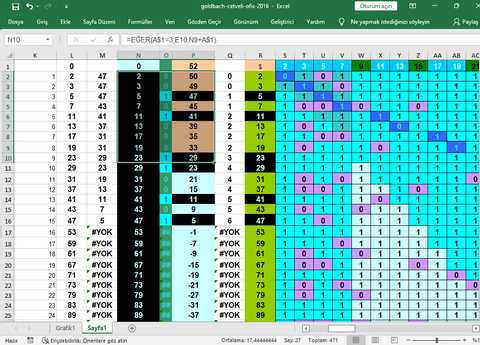
  • BEN CEVAP YAZARKEN ALTAKİ CEVAP KISMINAMI BASTIM BİLMİYORUM ÜSTTEKİ O SORUYADA ŞİMDİ CEVAP YAZDIM. GOLDBACH SANISININ CEVABINA GELİNCE EĞER VERDİĞİM LİNKDEKİ DOSYAYI OKUDUYSANIZ ORADA ÇİFT SAYI DOĞRUSUNA ERASTONES KALBURU UYGULANIP BUNA BENZER BİR MODELLEME İLE HERHANGİ BİR TEST SAYISINDA ORTALAMA GOLDBACH DEĞERLERİNİ HESAPLIYORUM BU MODELLEMEYİDE FORMÜLE ETTİĞİMİZDE EN AZ GOLDBACH ASALI ÇİFTLERİNİN OLDUĞU TEST SAYILARINDA BİLE BİRDEN FAZLA GOLBACH ASAL ÇİFTİ OLACAĞINI GÖSTEREN BİR FORMÜL YAZIYORUM İSTERSENİZ EXCEL PROĞRAMINIDA ATABİLİRİM.
  • doktor0906 D kullanıcısına yanıt
    Çözüm derken, çözümü yapan kodu göndermelisiniz. Ayrıca kod en azından 1 özyineleme / recursion kullanmalı tümüye döngü / loop 'tan oluşmamalı.

    Örneğin özyineleme kullanarak C++ ile yazdığım kod

    C=1
    B=8
    A=9

    sonucunu veriyor. Kodu gönderebilirim ancak bunun için öncelikle en az bir kişinin kendi çözümünü göndermesi gerekiyor.

    < Bu ileti mini sürüm kullanılarak atıldı >
    • 
Sayfa: önceki 7891011
Sayfaya Git
Git
sonraki
- x
Bildirim
mesajınız kopyalandı (ctrl+v) yapıştırmak istediğiniz yere yapıştırabilirsiniz.
Hizmet kalitesi için çerezleri kullanabiliriz. DH’ye girerek kullanım izni vermiş sayılırsınız.
Anladım Veri Politikamız