|
Problem : Elimizde farklı türlerden 4 tane meyve fidesi var: Elma şeftali kayısı armut 3 tane de bahçemiz var: Bahçe1, Bahçe2, Bahçe3 Bahçelerin büyüklükleri farklı olduğundan farklı sayıda ağaç sığıyor her birine. Bahçe1'e 3 fidan dikebiliyoruz. Bahçe2 ve Bahçe3'e ise 2şer ağaç sığabiliyor Ağaçların meyvelerini satarak para kazanıyoruz. Her ağaç farklı bahçelerde farklı miktarda meyve veriyor, dolayısıyla farklı miktarda kar ettiriyor. Örneğin, elma ağacını Bahçe1 e dikersek yıllık 900 kazanıyoruz. Elmayı Bahçe2 ye dikersek 1200, Bahçe3 e dikersek 800 kazanıyoruz. Benzer şekilde hangi ağaç hangi bahçede kaç para kazanc sağlıyor aşağıdaki tabloda var. Tabloda görüldüğü gibi her ağacı her bahçeye dikemiyoruz. Örneğin Armut sadece Bahçe2 ye dikilebiliyor SORU: Maksimum para kazanmak için hangi ağacı hangi bahçeye dikeceğimizi bulan bir algoritma nasıl olmalıdır? Not: Bahçe sayısı sabit kabul edilebilir. Ağaç türleri (daha fazla ağaç türü olabilir, ama her türden tek ağaç olacak), bahçelerin kapasiteleri ve ağaçların her bahçedeki kazançları değişebilmektedir. Algoritmayı bu kriterlere göre geliştirmek gerekiyor Detaylar/kriterler: 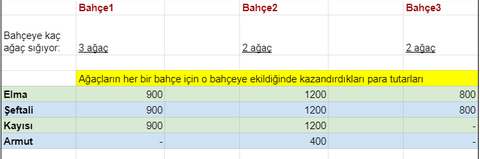 Örnek çözümler:   Yukardaki ikinci seçim en ideal çözüm. Ancak armutun bahçe2 deki kazancı 299 olsaydı birinci seçim en ideal çözüm olacaktı. < Bu mesaj bu kişi tarafından değiştirildi abars -- 17 Haziran 2021; 16:18:44 > |
Bu probleme algoritme geliştirebilir misiniz?

-
-
3 bahçe 4 meyve olduğu için brute-force algoritma iş görür. Yani her meyve için her bahçeyi sırayla deneyip maksimumu bulmak. Ama genel olarak m bahçe ve n meyve için düşünülürse maximum weighted bipartite matching kategorisine giriyor. Buna örnek olarak da Hungarian Algoritması verilebilir.
-
Öncelikle cevap için teşekkürler.
Ağaç sayısı değişken ve 200-300 olduğunda brute-force pek mümkün olmuyor.
Hungarian algoritmasını araştırıp anlamaya çalışıyorum ama genel olarak komplex duruyor.
Rica etsem doğrudan verdiğim probleme uygulaması nasıl olur anlatabilirseniz çok yardımı olur bana.
-
Çözümü kısmen buldum.
Lineer optimazasyon problemiymiş bu.
Google OR tools diye bi kütüphanesi varmış. Java ile com.google.ortools.linearsolver paketini kullanarak optimum sonucu bulan bir çözüm sağladım.
Ancak problem 200 300 agaç içerdiğinde performans ne olacak henüz denemedim.
-
Aslında bahçelerin de kapasitesi olduğunu gözardı etmişim. Bu durumda zaten karışık olan algoritma biraz daha karışıyor. Çünkü Hungarian algoritmasında bir bahçeye tek bir meyve ekilecek şekilde bulunuyordu sonuç. Bu durumda biraz daha genelleştirmek gerekiyor. Lineer programlama yapmak lazım gibi.
W(ij) = i. bahçeye j. meyvenin ekilmesi sonucu gelen kazanç olsun.
R(i) = i. bahçeye ekilebilecek maksimum fidan sayısı olsun.
x(ij) = i. bahçeye j. meyveyi ekip ekmediğimiz durumunu belirten parametre olsun.
Buna göre lineer program :
maksimumu bul -> her i ve j için toplam W(ij) * x(ij)
kısıtlar ise:
- her i için toplam x(ij) <= R(i), // bir bahçeye R(i)'a kadar meyve dikilebilir
- her j için toplam x(ij) = 1 // bir meyve sadece bir bahçeye dikilebilir.
- her x(ij) = 0 veya 1 olabilir. Aslında 2. kısıt bunu sağlıyor. x(ij) >= 0 da diyebiliriz integer programlamaya uygun olarak.
Edit : Sayfayı yenilemediğim için mesajını görmemişim. Sayı arttıkça tabi çözüm zamanı ne kadar uzayacak görmek lazım.
< Bu mesaj bu kişi tarafından değiştirildi yesil1026 -- 20 Haziran 2021; 15:20:11 >
Bu mesaj IP'si ile atılan mesajları ara Bu kullanıcının son IP'si ile atılan mesajları ara Bu mesaj IP'si ile kullanıcı ara Bu kullanıcının son IP'si ile kullanıcı ara
KAPAT X






 Yeni Kayıt
Yeni Kayıt







 Konudaki Resimler
Konudaki Resimler



 Hızlı
Hızlı 



















